How do we compose the network that performs the requisite function?
Preliminary
The bias can also be viewed as the weight of another input component that is always set to 1
z=∑iwixi
What we learn: The ..parameters.. of the network
Learning the network: Determining the values of these parameters such that the network computes the desired function
How to learn a network?
- W=Wargmin∫Xdiv(f(X;W),g(X))d
- div() is a divergence function thet goes to zero when f(X;W)=g(X)
But in practice g(x) will not have such specification
- Sample g(x): just gather training data
Learning
Simple perceptron
do For i=1..Ntrain
O(xi)=sign(WTXi)
if O(xi)≠yi
W=W+YiXi
until no more classification errors
A more complex problem
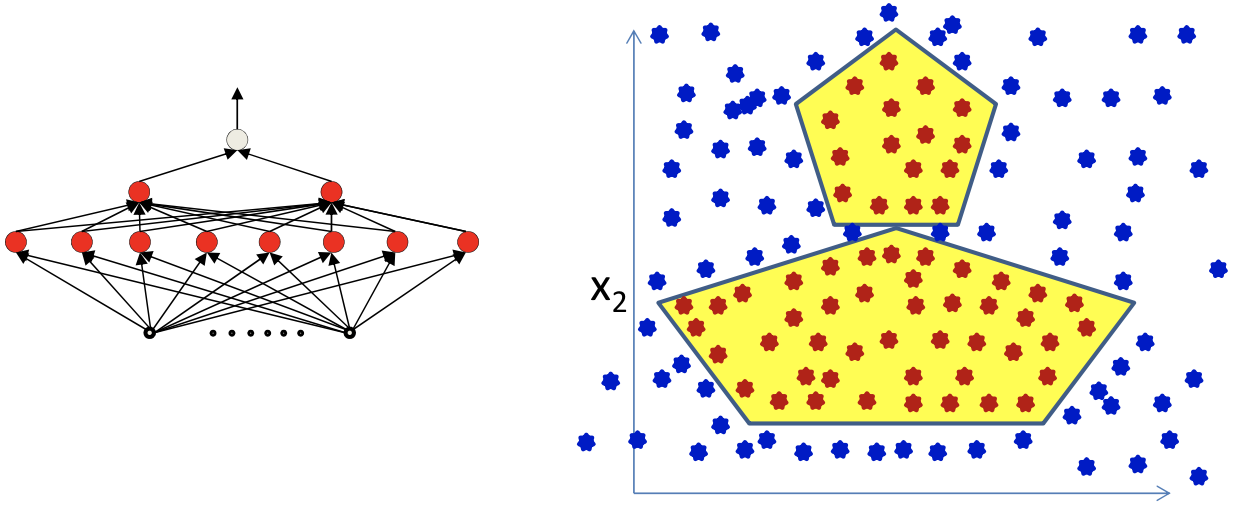
- This can be perfectly represented using an MLP
- But perveptron algorithm require linearly separated labels to be learned in lower-level neurons
- An exponential search over inputs
- So we need differentiable function to compute the change in the output for ..small.. changes in either the input or the weights
Empirical Risk Minimization
Assuming X is a random variable:
W=Wargmin∫Xdiv(f(X;W),g(X))P(X)dX=WargminE[div(f(X;W),g(X))]
Sample g(X), where di=g(Xi)+noise, estimate function from the samples
The empirical estimate of the expected error is the average error over the samples
E[div(f(X;W),g(X))]≈N1i=1∑Ndiv(f(Xi;W),di)
Empirical average error (Empirical Risk) on all training data
Loss(W)=N1i∑div(f(Xi;W),di)
Estimate the parameters to minimize the empirical estimate of expected error
W=WargminLoss(W)
Problem statement
- Given a training set of input-output pairs
(X_1,d_1),(X_2,d_2),…,(X_N,d_N)
- Minimize the following function
Loss(W)=N1i∑div(f(Xi;W),di)
- This is problem of function minimization
- An instance of optimization
